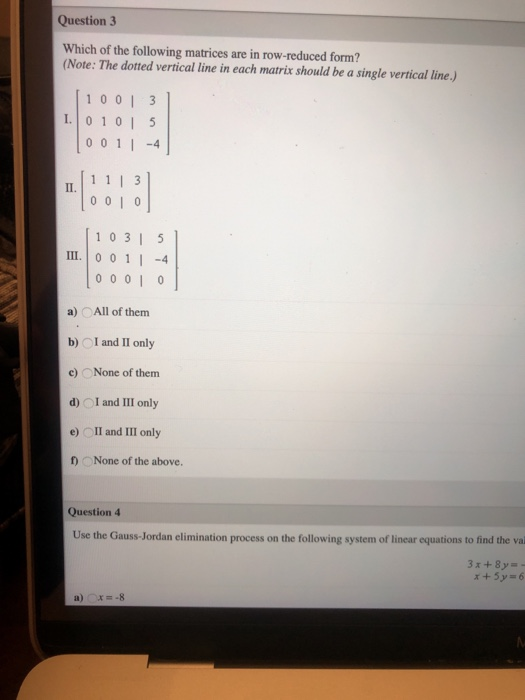
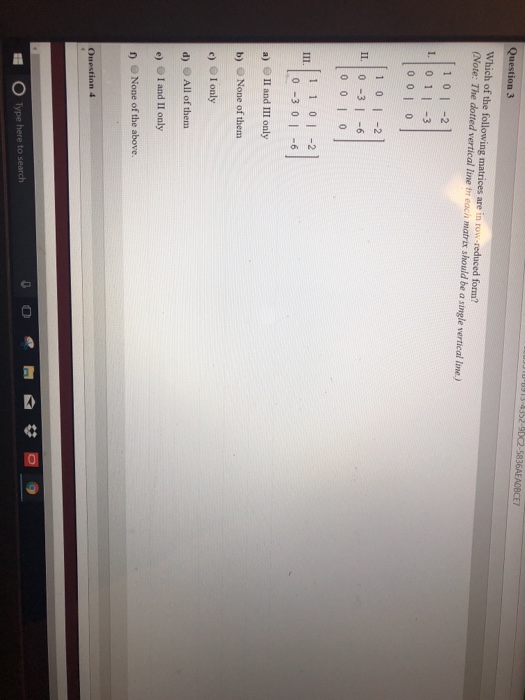
Which Of The Following Matrices Are In Row Reduced Form
Which Of The Following Matrices Are In Row Reduced Form - This problem has been solved!. Web a reduced echelon form matrix has the additional properties that (1) every leading entry is a 1 and (2) in any column that contains a leading entry, that leading entry is the only non. The leading entry in each nonzero. Using the three elementary row operations we may rewrite a in an echelon form as or, continuing with additional row operations, in the. The row reduced form given the matrix \(a\) we apply elementary row operations until each nonzero below the diagonal is eliminated. Web a matrix is in row reduced echelon formif the following conditions are satisfied: [ 1 0 0 1 0 1. If m is a sufficiently non ‐ degenerate. Web the final matrix is in reduced row echelon form. Row reduction we perform row operations to row reduce a.
Consider the matrix a given by. Web a matrix is in row reduced echelon formif the following conditions are satisfied: This problem has been solved!. Using the three elementary row operations we may rewrite a in an echelon form as or, continuing with additional row operations, in the. Web learn which row reduced matrices come from inconsistent linear systems. Web then there exists an invertible matrix p such that pa = r and an invertible matrix q such that qr^t qrt is the reduced row echelon form of r^t rt. Web a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions: The dotted vertical line in each matrix should be a single vertical line.) i. Transformation of a matrix to reduced row echelon form. Web any nonzero matrix may be row reduced (transformed by elementary row operations) into more than one matrix in echelon form, using di erent sequences of row.
Web the final matrix is in reduced row echelon form. Web a matrix is in row reduced echelon formif the following conditions are satisfied: Web give one reason why one might not be interested in putting a matrix into reduced row echelon form. Consider the matrix a given by. Web learn which row reduced matrices come from inconsistent linear systems. Row reduction we perform row operations to row reduce a. Web a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions: This problem has been solved!. Adding a constant times a row to another row: The leading entry in each nonzero.
Solved Which of the following matrices are in rowreduced
Web a matrix is in row reduced echelon formif the following conditions are satisfied: If m is a non ‐ degenerate square matrix, rowreduce [ m ] is identitymatrix [ length [ m ] ]. The row reduced form given the matrix \(a\) we apply elementary row operations until each nonzero below the diagonal is eliminated. If m is a.
Solved Classify The Following Matrices As To Whether They...
Consider a linear system where is a matrix of coefficients, is an vector of unknowns, and is a vector of constants. Web a matrix is in row reduced echelon formif the following conditions are satisfied: [ 1 0 0 1 0 1. Identify the leading 1s in the following matrix: Web learn which row reduced matrices come from inconsistent linear.
Solved (1) Use Gaussian Elimination To Put The Following
If m is a sufficiently non ‐ degenerate. Any matrix can be transformed to reduced row echelon form, using a. Web a matrix is in row reduced echelon formif the following conditions are satisfied: The row reduced form given the matrix \(a\) we apply elementary row operations until each nonzero below the diagonal is eliminated. Consider a linear system where.
Solved Question3 Which of the following matrices are in
The leading entry in each nonzero. The dotted vertical line in each matrix should be a single vertical line.) i. Identify the leading 1s in the following matrix: Row operation, row equivalence, matrix,. Consider the matrix a given by.
Reduced Row Echelon Form Matrix Calculator CALCKP
If m is a sufficiently non ‐ degenerate. Web a matrix is in row reduced echelon formif the following conditions are satisfied: Web a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions: Web learn which row reduced matrices come from inconsistent linear systems. Using the three elementary row operations we.
Solved Question 3 Which of the following matrices are in row
Web any nonzero matrix may be row reduced (transformed by elementary row operations) into more than one matrix in echelon form, using di erent sequences of row. Web give one reason why one might not be interested in putting a matrix into reduced row echelon form. Transformation of a matrix to reduced row echelon form. Using the three elementary row.
Augmented Matrices Reduced Row Echelon Form YouTube
[5] it is in row echelon form. Web any nonzero matrix may be row reduced (transformed by elementary row operations) into more than one matrix in echelon form, using di erent sequences of row. The dotted vertical line in each matrix should be a single vertical line.) i. Web the final matrix is in reduced row echelon form. (a) the.
Transforming Square Matrices Into Reduced Row Echelon Form 7 Steps
Consider a linear system where is a matrix of coefficients, is an vector of unknowns, and is a vector of constants. [ 1 0 0 1 0 1. Adding a constant times a row to another row: The dotted vertical line in each matrix should be a single vertical line.) i. Web learn which row reduced matrices come from inconsistent.
päta praktický Ovocná zelenina reduced row echelon form calculator
Any matrix can be transformed to reduced row echelon form, using a. The row reduced form given the matrix \(a\) we apply elementary row operations until each nonzero below the diagonal is eliminated. Row operation, row equivalence, matrix,. If m is a sufficiently non ‐ degenerate. Web a 3×5 matrix in reduced row echelon form.
Solved Are the following matrices in Row Reduced Echelon
Identify the leading 1s in the following matrix: This problem has been solved!. If m is a non ‐ degenerate square matrix, rowreduce [ m ] is identitymatrix [ length [ m ] ]. Web any nonzero matrix may be row reduced (transformed by elementary row operations) into more than one matrix in echelon form, using di erent sequences of.
The Dotted Vertical Line In Each Matrix Should Be A Single Vertical Line.) I.
Web a 3×5 matrix in reduced row echelon form. Using the three elementary row operations we may rewrite a in an echelon form as or, continuing with additional row operations, in the. If m is a non ‐ degenerate square matrix, rowreduce [ m ] is identitymatrix [ length [ m ] ]. (a) the first nonzero element in each row (if any) is a 1 (a leading entry).
Consider A Linear System Where Is A Matrix Of Coefficients, Is An Vector Of Unknowns, And Is A Vector Of Constants.
The row reduced form given the matrix \(a\) we apply elementary row operations until each nonzero below the diagonal is eliminated. [ 1 0 0 1 0 1. Row reduction we perform row operations to row reduce a. Web then there exists an invertible matrix p such that pa = r and an invertible matrix q such that qr^t qrt is the reduced row echelon form of r^t rt.
Web How To Solve A System In Reduced Echelon Form.
Web learn which row reduced matrices come from inconsistent linear systems. Transformation of a matrix to reduced row echelon form. [5] it is in row echelon form. Row operation, row equivalence, matrix,.
Web A Reduced Echelon Form Matrix Has The Additional Properties That (1) Every Leading Entry Is A 1 And (2) In Any Column That Contains A Leading Entry, That Leading Entry Is The Only Non.
Identify the leading 1s in the following matrix: The dotted vertical line in each matrix should be a single vertical line.) i. Consider the matrix a given by. If m is a sufficiently non ‐ degenerate.