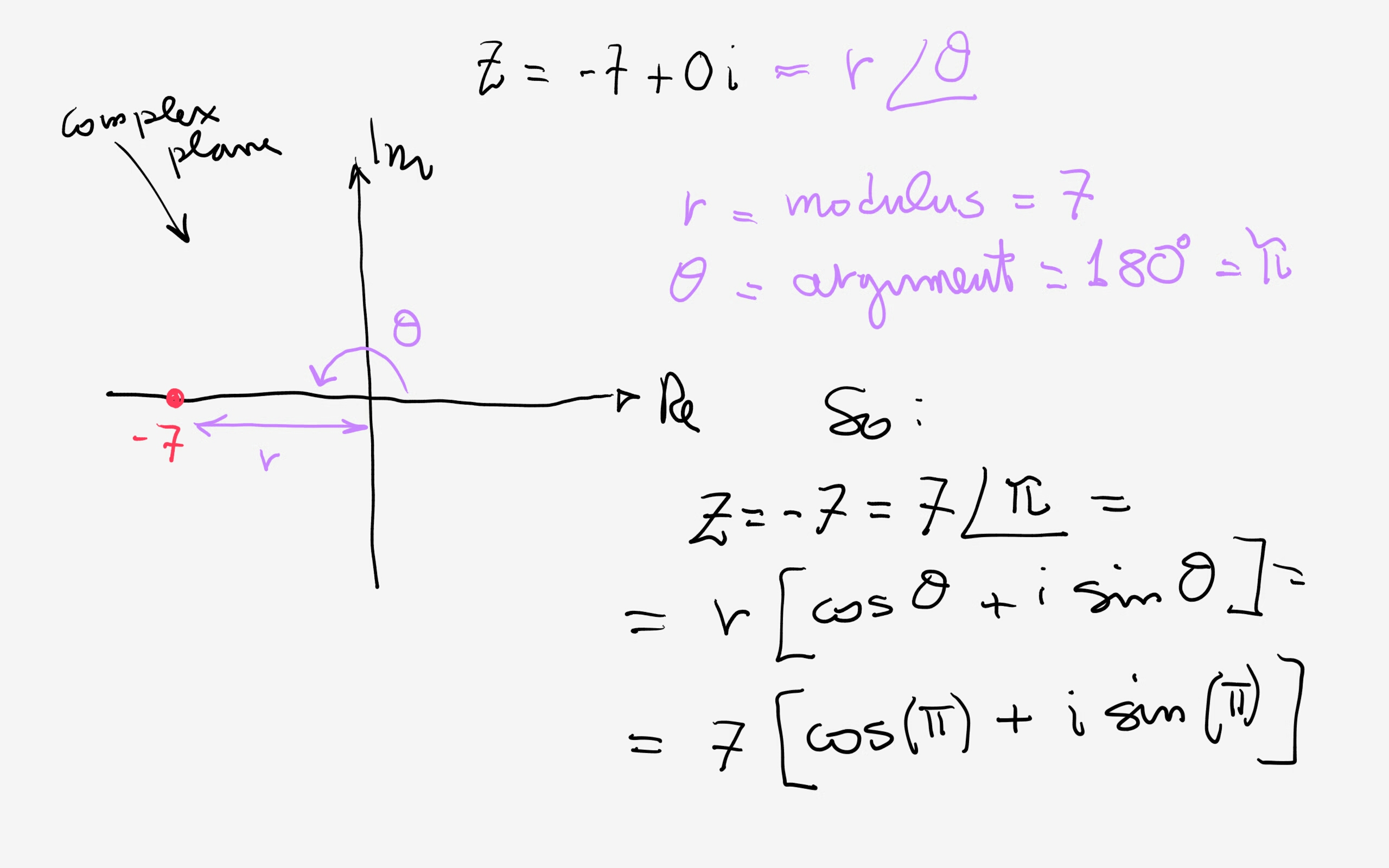Vector Trigonometric Form
Vector Trigonometric Form - The common types of vectors are cartesian vectors, column vectors, row vectors, unit vectors, and position vectors. ˆu = < 2,5 >. Web how to write a component form vector in trigonometric form (using the magnitude and direction angle). Express w as the sum of a horizontal vector, , w x, and a vertical vector,. Using trigonometry the following relationships are revealed. The figures below are vectors. We will also be using these vectors in our example later. $$ \| \vec{v} \| = \sqrt{v_1^2 + v_2^2 } $$ example 01: $$ \| \vec{v} \| = \sqrt{4^2 + 2 ^2} = \sqrt{20} = 2\sqrt{5} $$ Web what are the types of vectors?
Web when finding the magnitude of the vector, you use either the pythagorean theorem by forming a right triangle with the vector in question or you can use the distance formula. Web what are the types of vectors? We will also be using these vectors in our example later. Since displacement, velocity, and acceleration are vector quantities, we can analyze the horizontal and vertical components of each using some trigonometry. One way to represent motion between points in the coordinate plane is with vectors. It's a fairly clear and visual way to show the magnitude and direction of a vector on a graph. Write the word or phrase that best completes each statement or answers the question. Use inverse trigonometric functions to find the solutions, and check for extraneous solutions. Express w as the sum of a horizontal vector, , w x, and a vertical vector,. Web to find the direction of a vector from its components, we take the inverse tangent of the ratio of the components:
The formula is still valid if x is a complex number, and so some authors refer to the more general complex version as euler's. 10 cos120°,sin120° find the component form of the vector representing velocity of an airplane descending at 100 mph at 45° below the horizontal. Web a vector is defined as a quantity with both magnitude and direction. It's a fairly clear and visual way to show the magnitude and direction of a vector on a graph. This is much more clear considering the distance vector that the magnitude of the vector is in fact the length of the vector. Since displacement, velocity, and acceleration are vector quantities, we can analyze the horizontal and vertical components of each using some trigonometry. Web to find the direction of a vector from its components, we take the inverse tangent of the ratio of the components: Web how to write a component form vector in trigonometric form (using the magnitude and direction angle). In the above figure, the components can be quickly read. −→ oa and −→ ob.
Trig Polar/Trigonometric Form of a Complex Number YouTube
The vector in the component form is v → = 〈 4 , 5 〉. $$v_x = \lvert \overset{\rightharpoonup}{v} \rvert \cos θ$$ $$v_y = \lvert \overset{\rightharpoonup}{v} \rvert \sin θ$$ $$\lvert \overset{\rightharpoonup}{v} \rvert = \sqrt{v_x^2 + v_y^2}$$ $$\tan θ = \frac{v_y}{v_x}$$ In this example we have $ v_1 = 4 $ and $ v_2 = 2 $ so the magnitude is:.
The Product and Quotient of Complex Numbers in Trigonometric Form YouTube
Using trigonometry the following relationships are revealed. Web to better understand the product of complex numbers, we first investigate the trigonometric (or polar) form of a complex number. This is much more clear considering the distance vector that the magnitude of the vector is in fact the length of the vector. We will also be using these vectors in our.
Vectors in Trigonmetric Form YouTube
This complex exponential function is sometimes denoted cis x (cosine plus i sine). Adding vectors in magnitude & direction form. In this example we have $ v_1 = 4 $ and $ v_2 = 2 $ so the magnitude is: Web to solve a trigonometric simplify the equation using trigonometric identities. We will also be using these vectors in our.
How do you write the complex number in trigonometric form 7? Socratic
One way to represent motion between points in the coordinate plane is with vectors. Write the word or phrase that best completes each statement or answers the question. 10 cos120°,sin120° find the component form of the vector representing velocity of an airplane descending at 100 mph at 45° below the horizontal. Two vectors are shown below: Amy wants to push.
PPT Introduction to Biomechanics and Vector Resolution PowerPoint
The vector in the component form is v → = 〈 4 , 5 〉. Web the vector and its components form a right triangle. 11/18/2021 what is a vector? One way to represent motion between points in the coordinate plane is with vectors. $$v_x = \lvert \overset{\rightharpoonup}{v} \rvert \cos θ$$ $$v_y = \lvert \overset{\rightharpoonup}{v} \rvert \sin θ$$ $$\lvert \overset{\rightharpoonup}{v}.
Pc 6.3 notes_vectors
Write the result in trig form. Web where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex.
Trig Form of a Vector YouTube
Both component form and standard unit vectors are used. The formula for magnitude of a vector $ \vec{v} = (v_1, v_2) $ is: Web how to write a component form vector in trigonometric form (using the magnitude and direction angle). $$ \| \vec{v} \| = \sqrt{v_1^2 + v_2^2 } $$ example 01: Web to better understand the product of complex.
Vector Components Trigonometry Formula Sheet Math words, Math quotes
Web to better understand the product of complex numbers, we first investigate the trigonometric (or polar) form of a complex number. Web the vector and its components form a right angled triangle as shown below. Both component form and standard unit vectors are used. Web where e is the base of the natural logarithm, i is the imaginary unit, and.
Trigonometric Form To Standard Form
Web where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. Using trigonometry the following relationships are revealed. Use inverse trigonometric functions to find the solutions, and check for extraneous solutions. The formula for magnitude of a vector $ \vec{v} = (v_1, v_2) $.
Trigonometric Form To Polar Form
The formula for magnitude of a vector $ \vec{v} = (v_1, v_2) $ is: 10 cos120°,sin120° find the component form of the vector representing velocity of an airplane descending at 100 mph at 45° below the horizontal. Both component form and standard unit vectors are used. $$ \| \vec{v} \| = \sqrt{v_1^2 + v_2^2 } $$ example 01: Then, write.
Web The Vector And Its Components Form A Right Triangle.
Web where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. The figures below are vectors. 10 cos120°,sin120° find the component form of the vector representing velocity of an airplane descending at 100 mph at 45° below the horizontal. This is much more clear considering the distance vector that the magnitude of the vector is in fact the length of the vector.
Write The Word Or Phrase That Best Completes Each Statement Or Answers The Question.
Web what are the types of vectors? Adding vectors in magnitude & direction form. Web a vector is defined as a quantity with both magnitude and direction. Since displacement, velocity, and acceleration are vector quantities, we can analyze the horizontal and vertical components of each using some trigonometry.
A Vector Is Essentially A Line Segment In A Specific Position, With Both Length And Direction, Designated By An Arrow On Its End.
Web to better understand the product of complex numbers, we first investigate the trigonometric (or polar) form of a complex number. This complex exponential function is sometimes denoted cis x (cosine plus i sine). Find the magnitude of the vector $ \vec{v} = (4, 2) $. Web vectors in trigonmetric form demystifyingmath 710 subscribers subscribe 8 share 2.1k views 10 years ago trigonometry linear combination of vectors, vectors in.
The Common Types Of Vectors Are Cartesian Vectors, Column Vectors, Row Vectors, Unit Vectors, And Position Vectors.
Magnitude & direction form of vectors. ˆu = < 2,5 >. Web to find the direction of a vector from its components, we take the inverse tangent of the ratio of the components: A vector u has magnitude 2 and direction , θ = 116 ∘, where θ is in standard position.