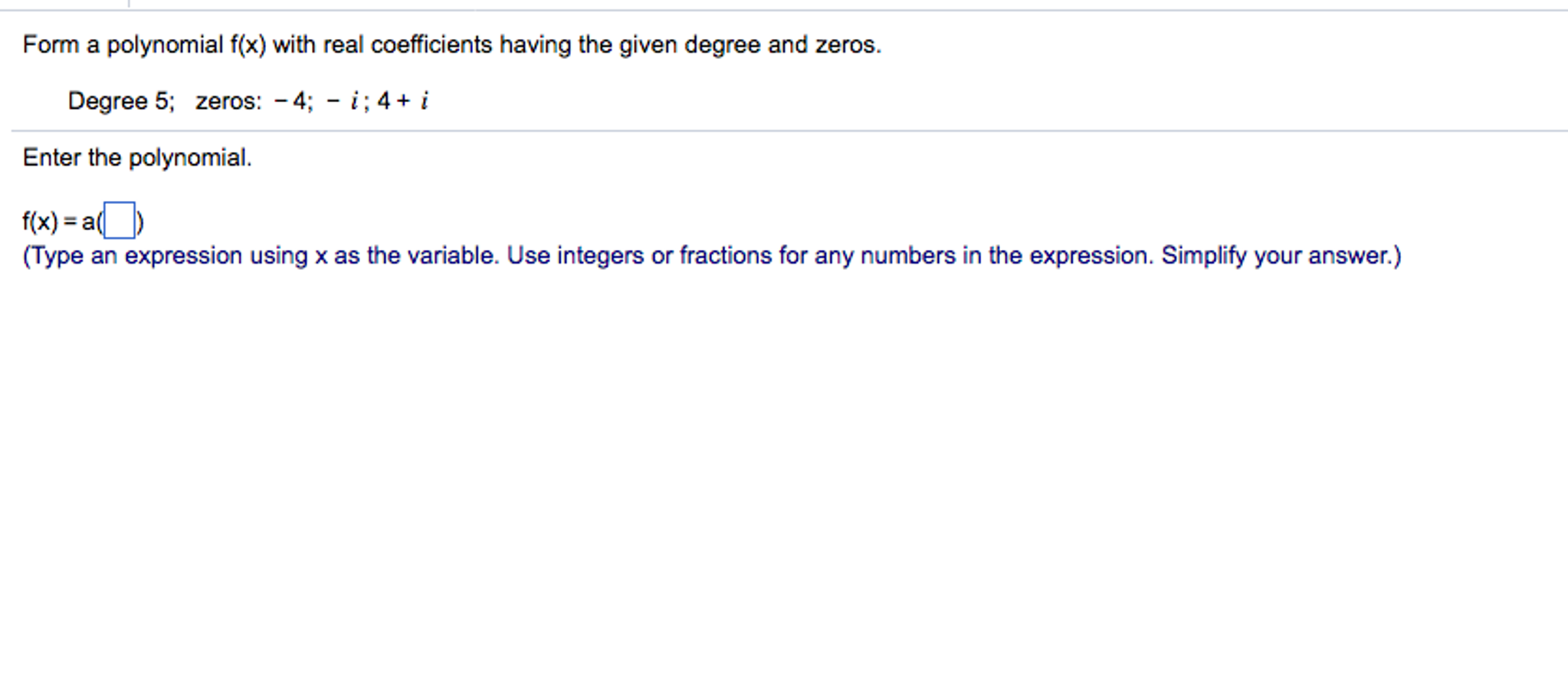
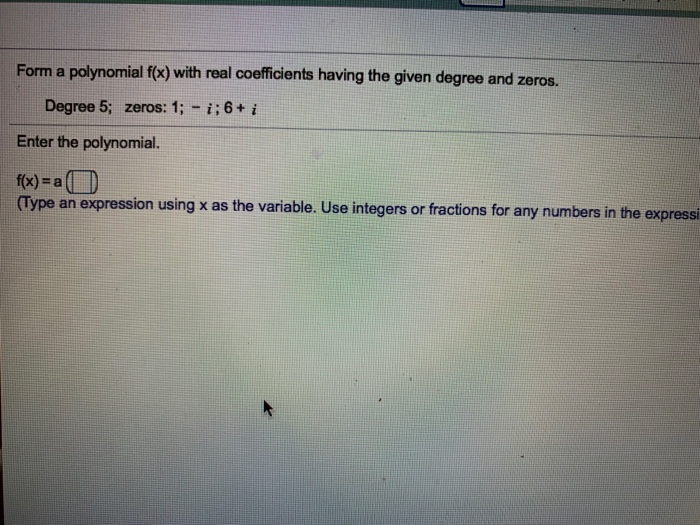
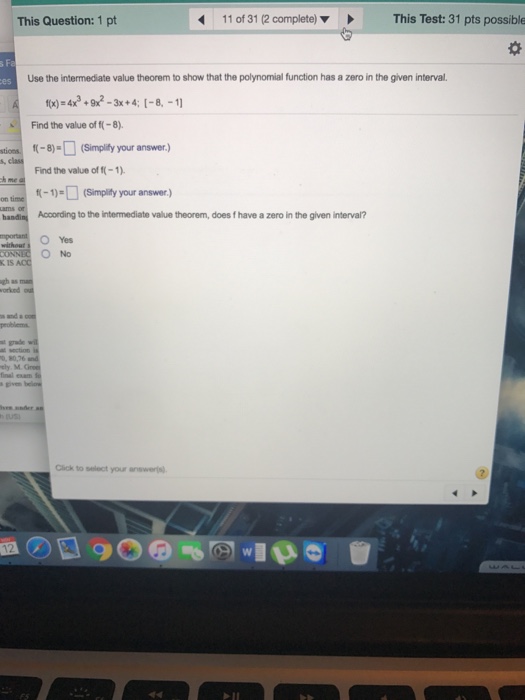
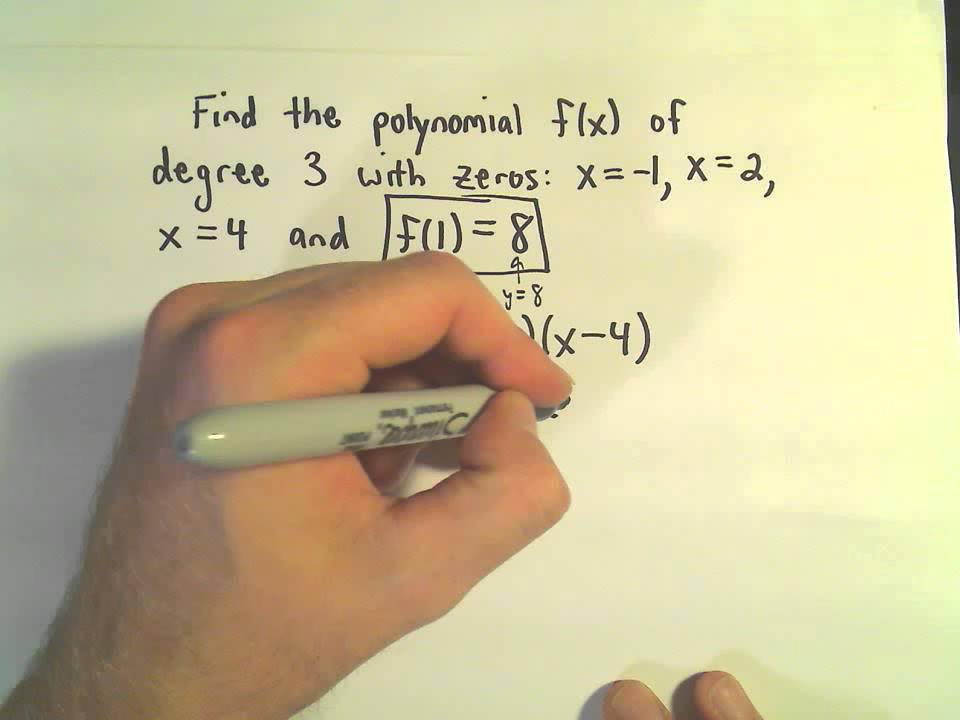Form A Polynomial With Given Zeros And Degree
Form A Polynomial With Given Zeros And Degree - Form a polynomial whose zeros and degree. 3 form a polynomial whose real zeros and. Which polynomial has a double zero of and. A polynomial function whose zeros are α, β, γ and δ and multiplicities are p, q, r and s respectively is. Further polynomials with the same zeros can be found by multiplying the simplest. Find the polynomial with integer coefficients having zeroes and. Form a polynomial whose zeros and degree are given. We can use this theorem to argue that, if f(x) is a. Form a polynomial f(x) with real coefficients having the given degree and zeros. (x −α)p(x − β)q(x − γ)r(x −δ)s.
Web 3 rows example: 3 form a polynomial whose real zeros and. Web make polynomial from zeros. A polynomial p p p p has zeros when x = 5 x=5 x = 5 x, equals, 5, x =. Factor it and set each factor to zero. Form a polynomial whose zeros and degree are given. Web so, how can one form a polynomial with given zeros and degree? A polynomial function whose zeros are α, β, γ and δ and multiplicities are p, q, r and s respectively is. Find the polynomial with integer coefficients having zeroes and. If for example, the zeros are a, b, and c, then the factors are, and thus the polynomial is,(x.
Web so first you need the degree of the polynomial, or in other words the highest power a variable has. Find the polynomial with integer coefficients having zeroes and. The definition also holds if the coefficients are complex, but that’s a topic for a more advanced course. Web to solve a polynomial equation write it in standard form (variables and canstants on one side and zero on the other side of the equation). Web the fundamental theorem of algebra states that, if f(x) is a polynomial of degree n > 0, then f(x) has at least one complex zero. Form a polynomial f(x) with real coefficients having the given degree and zeros. Web math precalculus precalculus questions and answers form a polynomial whose zeros and degree are given. (x −α)p(x − β)q(x − γ)r(x −δ)s. Create the term of the simplest polynomial from the given zeros. Web form a polynomial whose real zeros and degree are given.
Form A Polynomial With Given Zeros And Degree Mathway ultimatefushion
To write a polynomial function which has given zeros, take each zero and create a factor of the. Form a polynomial f(x) with real coefficients having the given degree and zeros. Form a poly mromall whoge zeros and degrees are given, use leading coefficont of 7 2 eros 0,−3,2; So if the leading term has an x^4 that means at.
Solved Form a polynomial whose real zeros and degree are
Web 3 rows example: Web we say that a is a zero of the polynomial if and only if p(a) = 0. Web form a polynomial whose real zeros and degree are given. If for example, the zeros are a, b, and c, then the factors are, and thus the polynomial is,(x. Web make polynomial from zeros.
newtonslabdesign Polynomial Of Degree 3
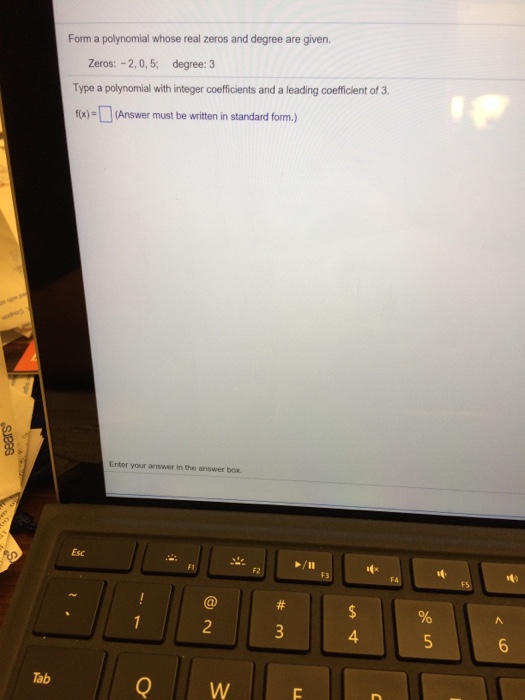
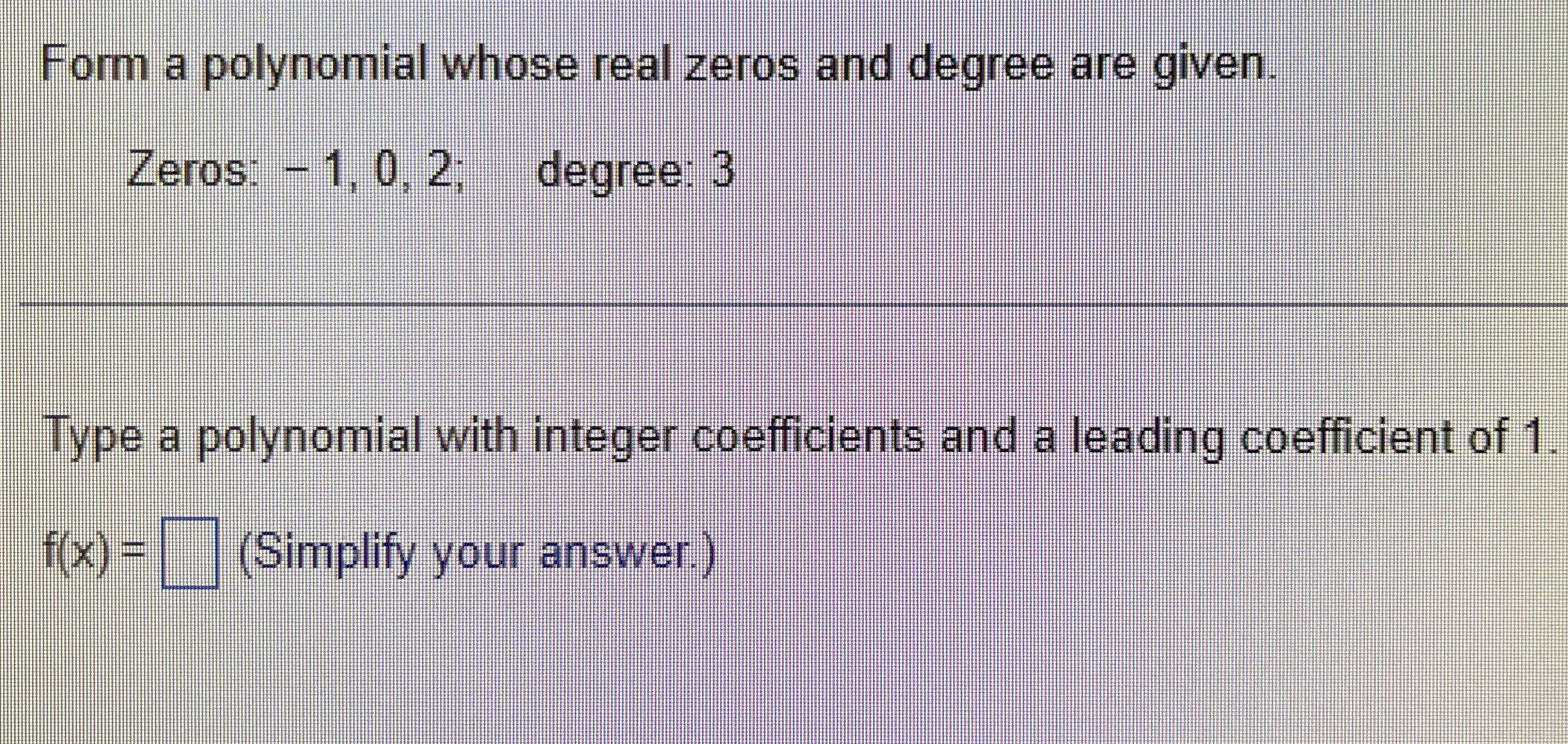
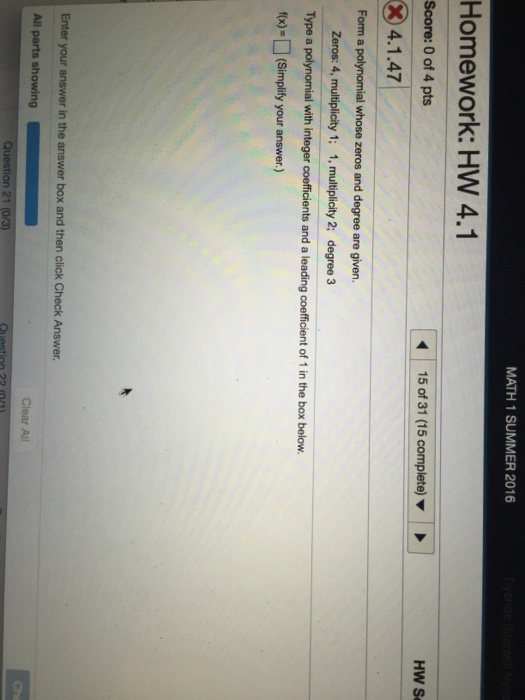
3 type a polynomial with integer coefficients and a leading coefficient of 1 in the box. Web the fundamental theorem of algebra states that, if f(x) is a polynomial of degree n > 0, then f(x) has at least one complex zero. Type a polynomial with integer coefficients and a leading coefficient of 1. Form a polynomial whose zeros and.
Form a polynomial whose real zeros and degree are CameraMath
What is the simplified form of 4 log3y. Find the polynomial with integer coefficients having zeroes and. Further polynomials with the same zeros can be found by multiplying the simplest. Form a polynomial whose zeros and degree are given. By the fundamental theorem of algebra, since the degree of the polynomial is 4 the polynomial has 4 zeros if you.
Precalculus Archive July 06, 2016
Web to solve a polynomial equation write it in standard form (variables and canstants on one side and zero on the other side of the equation). Further polynomials with the same zeros can be found by multiplying the simplest. Web form a polynomial with the given zeros example problems with solutions. If for example, the zeros are a, b, and.
Form A Polynomial With Given Zeros And Degree Mathway ultimatefushion
Form a poly mromall whoge zeros and degrees are given, use leading coefficont of 7 2 eros 0,−3,2; Find the polynomial with integer coefficients having zeroes and. Form the quadratic polynomial whose zeros are 4 and 6. So if the leading term has an x^4 that means at most there can be 4 0s. Form a polynomial whose zeros and.
Solved Form a polynomial f(x) with real coefficients having
If for example, the zeros are a, b, and c, then the factors are, and thus the polynomial is,(x. So if the leading term has an x^4 that means at most there can be 4 0s. 3 type a polynomial with integer coefficients and a leading coefficient of 1 in the box. What is the simplified form of 4 log3y..
Form a Polynomial with real Coefficients Given Degree And Zeros. 32i
Web answer (1 of 5): If you are given the zeros, then it is easy to find the polynomial. Form a polynomial whose zeros and degree. To write a polynomial function which has given zeros, take each zero and create a factor of the. Web make polynomial from zeros.
Solved Form a polynomial f(x) with real coefficients having
Form a polynomial whose zeros and degree. So if the leading term has an x^4 that means at most there can be 4 0s. Which polynomial has a double zero of and. Further polynomials with the same zeros can be found by multiplying the simplest. Factor it and set each factor to zero.
Solved Form a polynomial whose real zeros and degree are
Form a polynomial whose zeros and degree are given. Further polynomials with the same zeros can be found by multiplying the simplest. 3 form a polynomial whose real zeros and. 3 type a polynomial with integer coefficients and a leading coefficient of 1 in the box. A polynomial function whose zeros are α, β, γ and δ and multiplicities are.
So If The Leading Term Has An X^4 That Means At Most There Can Be 4 0S.
Web form a polynomial whose real zeros and degree are given. If for example, the zeros are a, b, and c, then the factors are, and thus the polynomial is,(x. Web so first you need the degree of the polynomial, or in other words the highest power a variable has. Web answer (1 of 5):
Web So, How Can One Form A Polynomial With Given Zeros And Degree?
The definition also holds if the coefficients are complex, but that’s a topic for a more advanced course. (x −α)p(x − β)q(x − γ)r(x −δ)s. Form a polynomial whose zeros and degree are given. If you are given the zeros, then it is easy to find the polynomial.
Factor It And Set Each Factor To Zero.
Form a polynomial f(x) with real coefficients having the given degree and zeros. Form the quadratic polynomial whose zeros are 4 and 6. Form a poly mromall whoge zeros and degrees are given, use leading coefficont of 7 2 eros 0,−3,2; Web the fundamental theorem of algebra states that, if f(x) is a polynomial of degree n > 0, then f(x) has at least one complex zero.
By The Fundamental Theorem Of Algebra, Since The Degree Of The Polynomial Is 4 The Polynomial Has 4 Zeros If You Count Multiplicity.
Find a polynomial that has zeros. We can use this theorem to argue that, if f(x) is a. Find the polynomial with integer coefficients having zeroes and. Further polynomials with the same zeros can be found by multiplying the simplest.