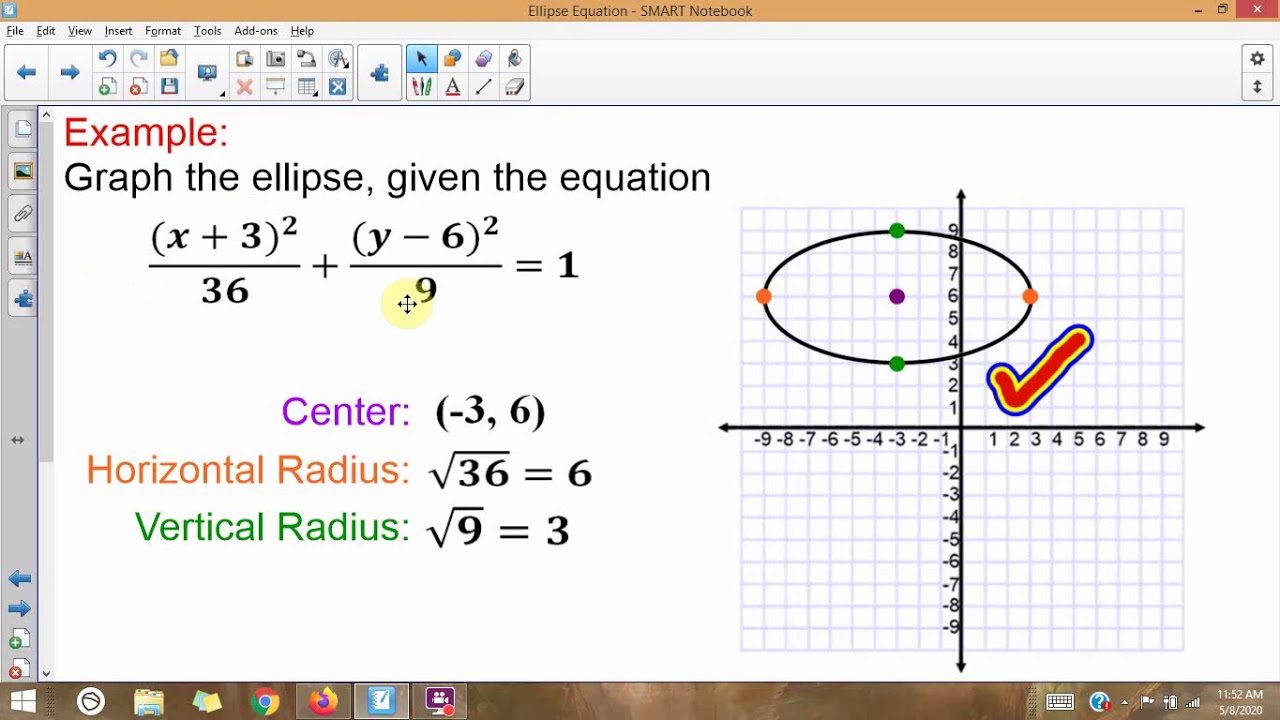
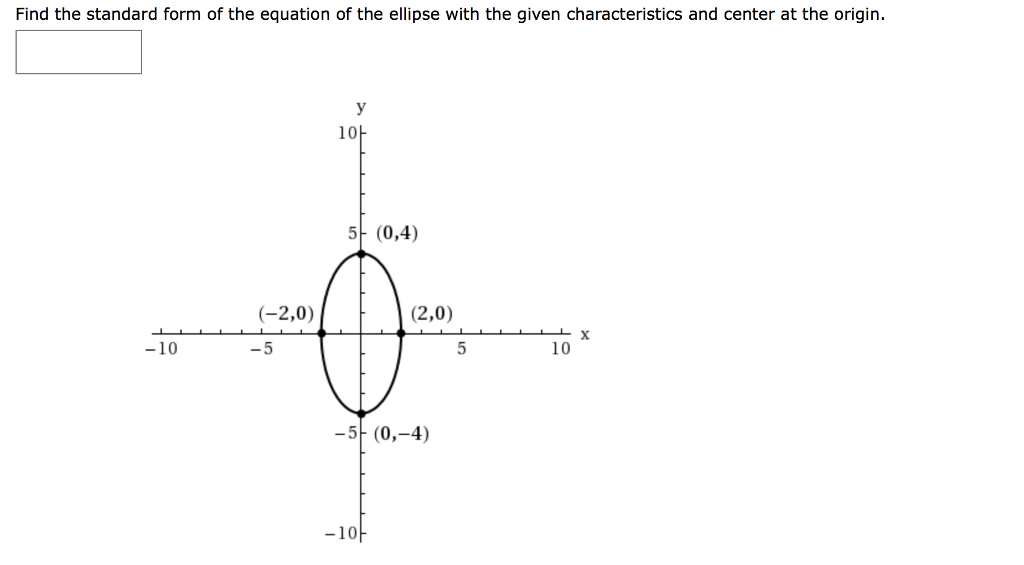
Find The Standard Form Of The Equation Of The Ellipse
Find The Standard Form Of The Equation Of The Ellipse - Top voted arunit baidya 7 years ago why is the equation always equal to 1? X2 b2 + y2 a2 =1 x 2 b 2 + y 2 a 2 = 1. 9x^2 + 16y^2 − 32y = 128; Questions tips & thanks want to join the conversation? Note that this is twice the distance from the center to the edge of the ellipse on the minor axis; 2/3 this problem has been solved! ( c1, c2) defines the coordinate of the center of the ellipse. You'll get a detailed solution from a subject matter expert that helps you learn core concepts. Web the ellipse equation in standard form involves the location of the ellipse's center and its size. Web find the standard form of the equation of the ellipse with the given characteristics.
( c1, c2) defines the coordinate of the center of the ellipse. ( x − h) 2 b 2 + ( y − k) 2 a 2 = 1 major axis is vertical. Web precalculus precalculus questions and answers find the standard form of the equation of the ellipse satisfying the following conditions. 9x^2 + 16y^2 − 32y = 128. Web given the general form of an equation for an ellipse centered at (h, k), express the equation in standard form. Web the general form for the standard form equation of an ellipse is shown below. Web notice at the top of the calculator you see the equation in standard form, which is. Web find the standard form of the equation of the ellipse with the given characteristics. A >b a > b. Web there are two general equations for an ellipse.
An ellipse is the set of all points (x, y) in a plane such that the sum of their distances from two fixed points is a constant. Web given the general form of an equation for an ellipse centered at (h, k), express the equation in standard form. Web find the standard form of the equation of the ellipse with the given characteristics. 9x^2 + 16y^2 − 32y = 128; The standard form for an ellipse centered at the origin is x²/a² + y²/b² = 1. Web equation of an ellipse. ( c1, c2) defines the coordinate of the center of the ellipse. Find the vertices and foci of the ellipse. Recognize that an ellipse described by an equation in the form a x 2 + b y 2 + c x + d y + e = 0 a x 2 + b y 2 + c x + d y + e = 0 is in general form. Top voted arunit baidya 7 years ago why is the equation always equal to 1?
Ex Write the General Equation of an Ellipse in Standard Form and Graph
This is the value referred to in the ellipse equation. Web precalculus precalculus questions and answers find the standard form of the equation of the ellipse satisfying the following conditions. You'll get a detailed solution from a subject matter expert that helps you learn core concepts. Web i bet your problem has been with the term minor axis. Find the.
Completing the Square to Write the Equation of an Ellipse in Standard
Web the ellipse equation in standard form involves the location of the ellipse's center and its size. A >b a > b. Web there are two general equations for an ellipse. ( x − h) 2 b 2 + ( y − k) 2 a 2 = 1 major axis is vertical. A = 4 a = 4
Equation of an Ellipse ( Video ) Calculus CK12 Foundation
Where e = eccentricity (0 < e < 1) foci : A >b a > b. Learn what the standard form of an ellipse equation is, how to identity the center and size of the. The coordinates of the vertices are (0,±a) ( 0, ± a) the length of the minor axis is 2b 2 b. ( x − h).
Equation of an Ellipse YouTube
Major axis vertical with length 10 ; Web find the standard form of the equation of the ellipse with the given characteristics. ( c1, c2) defines the coordinate of the center of the ellipse. Top voted arunit baidya 7 years ago why is the equation always equal to 1? The coordinates of the vertices are (0,±a) ( 0, ± a).
Ellipse (Definition, Equation, Properties, Eccentricity, Formulas)
Web i bet your problem has been with the term minor axis. Web simply speaking, when we stretch a circle in one direction to create an oval, that makes an ellipse. Length of minor axis =8; A 2 , b 2 , h , and k are all numbers that determine various characteristics about the ellipse. Web the equation of.
Ex Find Standard Form of an Equation of an Ellipse from a Graph
Web equation for an ellipse (standard form) here is the formula for an ellipse in standard form: 9x^2 + 16y^2 − 32y = 128. Find the vertices and foci of the ellipse. Web given the general form of an equation for an ellipse centered at (h, k), express the equation in standard form. A = 4 a = 4
Standard Form Equation Of An Ellipse What Is The Standard Form Of The
Web find the vertices and foci of the ellipse. X2 b2 + y2 a2 =1 x 2 b 2 + y 2 a 2 = 1. Web equation of an ellipse. Web learn all about ellipses in this video. A >b a > b.
Ellipse (h,k)
The video also explains how to. Questions tips & thanks want to join the conversation? Answer • 1 comment ( 27 votes) upvote downvote flag more Web find the vertices and foci of the ellipse. Web notice at the top of the calculator you see the equation in standard form, which is.
Ellipses Centered at the Origin ( Video ) Calculus CK12 Foundation
Web equation of an ellipse. Web the ellipse equation in standard form involves the location of the ellipse's center and its size. Want to learn more about ellipse equation? X2 b2 + y2 a2 =1 x 2 b 2 + y 2 a 2 = 1. Center coordinates (h, k) major axis 2a.
Solved Find the standard form of the equation of the ellipse
A 2 , b 2 , h , and k are all numbers that determine various characteristics about the ellipse. The standard form for an ellipse centered at the origin is x²/a² + y²/b² = 1. 0 < b < a. Web find the standard form of the equation of the ellipse with the given characteristics. The standard form of.
2/3 This Problem Has Been Solved!
( x − h) 2 b 2 + ( y − k) 2 a 2 = 1 major axis is vertical. Web precalculus precalculus questions and answers find the standard form of the equation of the ellipse satisfying the following conditions. Web standard equation of an ellipse: Web equation of an ellipse:
This Is The Value Referred To In The Ellipse Equation.
Want to learn more about ellipse equation? The standard form for an ellipse centered at the origin is x²/a² + y²/b² = 1. Web find the standard form of the equation of the ellipse with the given characteristics. Web simply speaking, when we stretch a circle in one direction to create an oval, that makes an ellipse.
A >B A > B.
Length of minor axis =8; Web find the vertices and foci of the ellipse. (2,7) the standard form of the equation is. The video also explains how to.
The Length Of The Major Axis Is 2A 2 A.
( x − h) 2 a 2 + ( y − k) 2 b 2 = 1 major axis is horizontal. A 2 , b 2 , h , and k are all numbers that determine various characteristics about the ellipse. Web how do you find the standard form of the equation of the ellipse given the properties center (5,2), vertex (0,2) and eccentricity 1/2? Find the vertices and foci of the ellipse.