Chapter 9 Right Triangles And Trigonometry Answer Key
Chapter 9 Right Triangles And Trigonometry Answer Key - Bugs bunny was 33 33 meters below ground, digging his way toward pismo beach, when he realized he wanted to be. Short leg = x, long leg = x√3, and hypotenuse = 2x. H ≈ 46.2 use a calculator. The cosine is just the sine of the complement of the angle in a right triangle, for example the. In a right triangle, the square of. Web introduction chapter 1 angles and their measure definitions and terminology complementary and supplementary angles coterminal angles and reference angles radian measure chapter 2 concepts from geometry the sum of a triangle’s angles and the triangle inequality the pythagorean theorem chapter 3 right triangle trigonometry trigonometric ratios of an acute angle in a right triangle. Web big ideas math geometry chapter 9: A = 7 tan ( 30°) ≈ 12.1 sin ( 30°) = 7 c c. Right triangles and trigonometry chapter exam. Getting ready for right triangles and trigonometry.
Using similarity to estimate ratio between side lengths. Another way to look at this sequence is to compare the ratios of the consecutive terms. Using right triangle ratios to approximate angle measure. Learn how to get it at muzing.org and review the. Legs = n and hypotenuse = n√2. Choose your answer to the question and click continue to see how you did. Then sin x = cos ( π 2 − x ). C = 7 sin ( 30°) = 14 57° 57°, h tan θ = opposite adjacent tan ( 57°) = h 30 solve for h. ∣ 4 ∣= 4 ∣ 6 + 4 ∣=∣ 10 ∣= 10 ∣ 2 − 9 ∣=∣ −7 ∣= 7 ∣ 7 −∣= −7 so, the order is − ∣ 7 ∣ ∣ 94 ∣ ∣ 2 − 9 ∣, and ∣ 6 + 4 ∣. 466 chapter 9 right triangles and trigonometry.
Then sin x = cos ( π 2 − x ). Getting ready for right triangles and trigonometry. In a right triangle, the square of. 36 4 95 15 solution let c represent the length of the longest side of the triangle. 466 chapter 9 right triangles and trigonometry. ∣ 9 − 3 ∣=∣ 6 ∣= 6 ∣ −4 ∣= 4 ∣20 ∣= 0 so, the length is 11 ∣−5 ∣ — ∣ 2 ∣ = 5 2 = 2.5 —so, the order is ∣ 0 ∣ ∣ −5 ∣ ∣ 2 ∣ , ∣ −4 ∣, and ∣ 9. Web 490 www.ck12.org chapter 9. Side ratios in right triangles as a function of the angles. Using right triangle ratios to approximate angle measure. We begin with the familiar pythagorean theorem, a 2 + b 2 =.
5 Resources for Right Triangles and Trigonometry
Using right triangle ratios to approximate angle measure. Web my pdf collection 2021 new book in pdf with fast download and very clear reolution updated daily chapter 9 right triangles and trigonometry answer key chapter 9 right triangles and trigonometry answer key. Web gradually the right triangle replaced the chords of circles as the basis of trigonometric definitions. H ≈.
Unit 8 Test Right Triangles And Trigonometry Answer Key Unit 8 Right
Side ratios in right triangles as a function of the angles. Right triangles and trigonometry chapter exam. Web introduction chapter 1 angles and their measure definitions and terminology complementary and supplementary angles coterminal angles and reference angles radian measure chapter 2 concepts from geometry the sum of a triangle’s angles and the triangle inequality the pythagorean theorem chapter 3 right.
PPT Chapter 9 Triangle Trigonometry PowerPoint Presentation, free
Evaluate the other five trigonometric functions of θ. Web viewing the two acute angles of a right triangle, if one of those angles measures x, x, the second angle measures π 2 − x. Viewing the two acute angles of a right triangle, if one of those angles measures. Using similarity to estimate ratio between side lengths. Web my pdf.
Unit 8 Right Triangles And Trigonometry Homework 5 Answer Key Home
Web 466 chapter 9 right triangles and trigonometry verifying right triangles tell whether each triangle is a right triangle. 466 chapter 9 right triangles and trigonometry. Viewing the two acute angles of a right triangle, if one of those angles measures. Using similarity to estimate ratio between side lengths. Web big ideas math geometry chapter 9:
Homework Answer Key Unit 8 Right Triangles And Trigonometry Unit 8
Web struggling with stoichiometry? Using right triangle ratios to approximate angle measure. Choose your answer to the question and click continue to see how you did. Web viewing the two acute angles of a right triangle, if one of those angles measures x, x, the second angle measures π 2 − x. Web my pdf collection 2021 new book in.
Chapter 8 Right Triangles and Trigonometry Answer Key
Then sin x = cos ( π 2 − x ). Short leg = x, long leg = x√3, and hypotenuse = 2x. Ratios in right triangles introduction to the trigonometric ratios solving for a side in a right triangle using the trigonometric ratios. Choose your answer to the question and click continue to see how you did. The cosine.
Unit 8 Test Right Triangles And Trigonometry Answer Key + My PDF
Web big ideas math geometry chapter 9: Ratios in right triangles introduction to the trigonometric ratios solving for a side in a right triangle using the trigonometric ratios. Using similarity to estimate ratio between side lengths. Bugs bunny was 33 33 meters below ground, digging his way toward pismo beach, when he realized he wanted to be. Getting ready for.
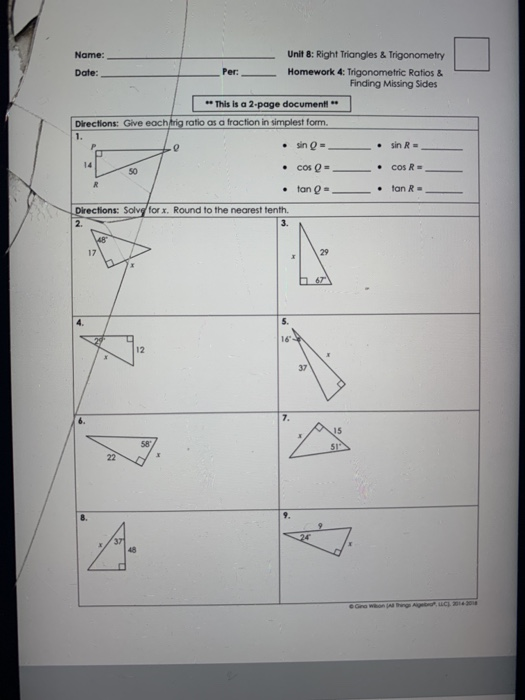
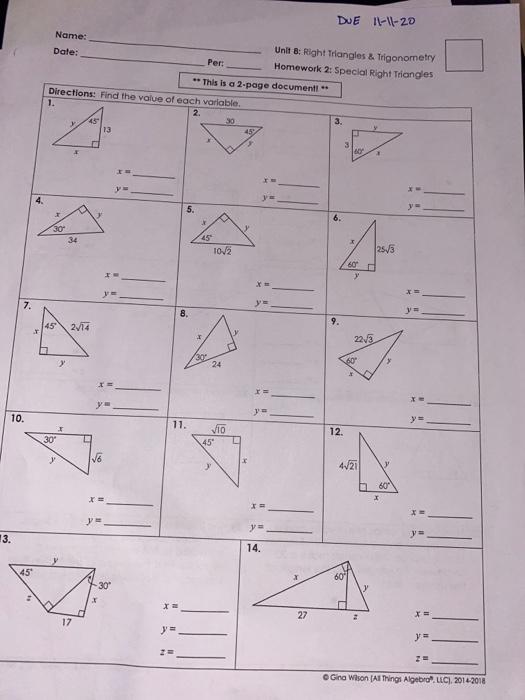
Solved DUE Il1120 Name Date Per Unit 8 Right Triangles
A ratio of two sides of a right triangle. Web right triangle trigonometry word problems. H = 30tan ( 57°) multiply. Choose your answer to the question and click continue to see how you did. Legs = n and hypotenuse = n√2.
Unit 8 Right Triangles And Trigonometry Key / Unit 8 Right Triangles
A = 7 tan ( 30°) ≈ 12.1 sin ( 30°) = 7 c c. 466 chapter 9 right triangles and trigonometry. H = 30tan ( 57°) multiply. Legs = n and hypotenuse = n√2. Getting ready for right triangles and trigonometry.
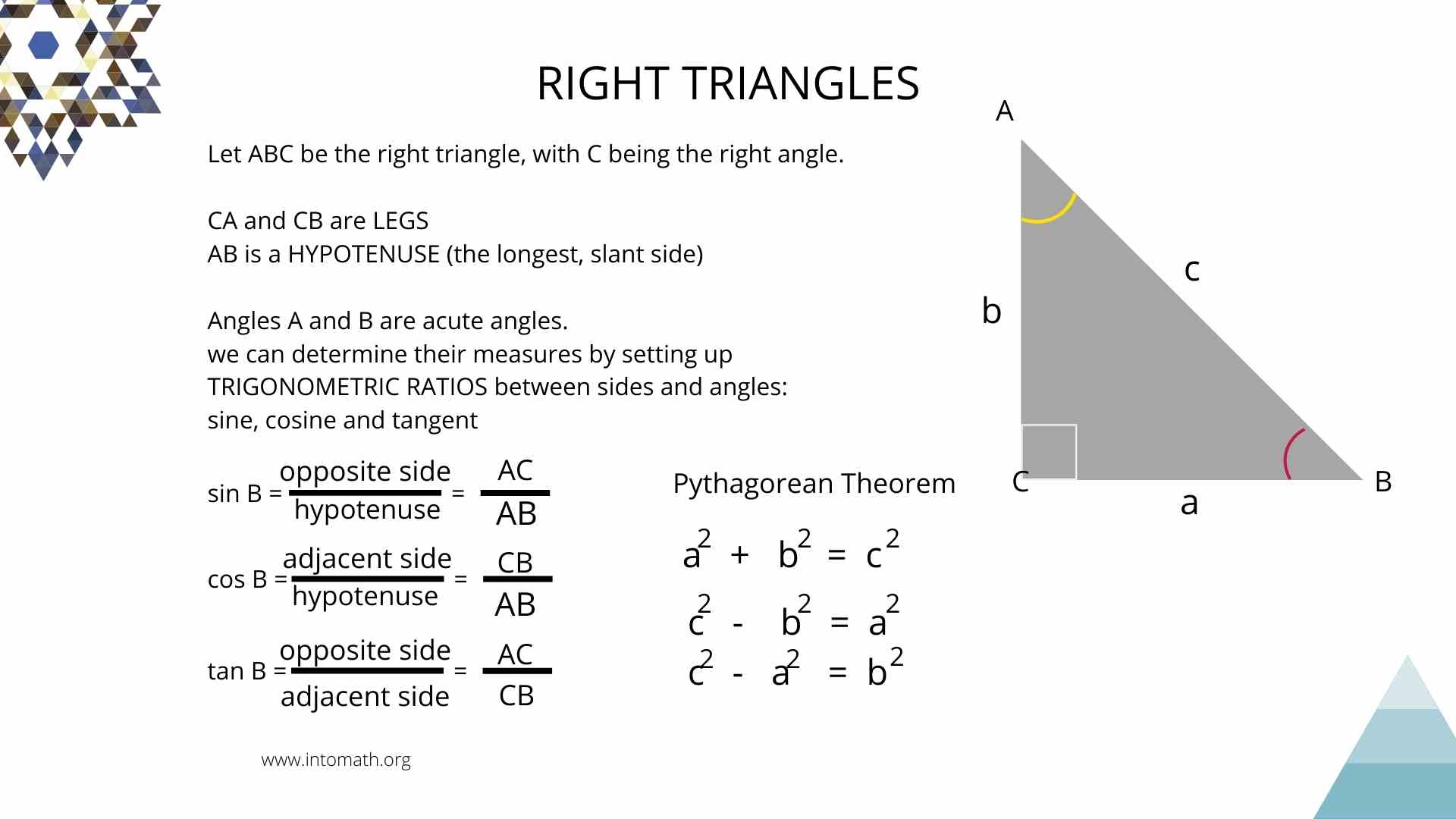
Lesson 5 Right Triangle Trigonometry. Trig ratios IntoMath
Web gradually the right triangle replaced the chords of circles as the basis of trigonometric definitions. Another way to look at this sequence is to compare the ratios of the consecutive terms. Side ratios in right triangles as a function of the angles. Using right triangle ratios to approximate angle measure. Evaluate the other five trigonometric functions of θ.
36 4 95 15 Solution Let C Represent The Length Of The Longest Side Of The Triangle.
Short leg = x, long leg = x√3, and hypotenuse = 2x. Our answer key can help. Another way to look at this sequence is to compare the ratios of the consecutive terms. Learn how to get it at muzing.org and review the.
A = 7 Tan ( 30°) ≈ 12.1 Sin ( 30°) = 7 C C.
Using right triangle ratios to approximate angle measure. Choose your answer to the question and click continue to see how you did. H = 30tan ( 57°) multiply. Web right triangle trigonometry word problems.
Web Big Ideas Math Geometry Chapter 9:
Right triangle trigonometry multiplied by 3 to get the next term in the sequence. Web 466 chapter 9 right triangles and trigonometry verifying right triangles tell whether each triangle is a right triangle. Evaluate the other five trigonometric functions of θ. ∣ 9 − 3 ∣=∣ 6 ∣= 6 ∣ −4 ∣= 4 ∣20 ∣= 0 so, the length is 11 ∣−5 ∣ — ∣ 2 ∣ = 5 2 = 2.5 —so, the order is ∣ 0 ∣ ∣ −5 ∣ ∣ 2 ∣ , ∣ −4 ∣, and ∣ 9.
Getting Ready For Right Triangles And Trigonometry.
Using similarity to estimate ratio between side lengths. ∣ 4 ∣= 4 ∣ 6 + 4 ∣=∣ 10 ∣= 10 ∣ 2 − 9 ∣=∣ −7 ∣= 7 ∣ 7 −∣= −7 so, the order is − ∣ 7 ∣ ∣ 94 ∣ ∣ 2 − 9 ∣, and ∣ 6 + 4 ∣. In a right triangle, θ is an acute angle and sin θ = \(\frac{1}{2}\). Legs = n and hypotenuse = n√2.